Om santi santi om.
Maksud ane kaya gini nih... (dalam dua dimensi) jadi orangnya bisa jalan menurut permukaan yang dia pijak
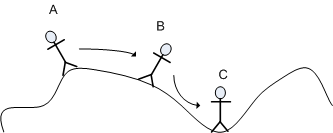
Salam kenal ... .

Permasalahan ini dapat diselesaikan dengan konsep koordinat umum, yaitu bahwa titik-titik pada suatu kurva memiliki satu koordinat umum, serta titik-titik pada suatu permukaan memiliki dua koordinat umum ... . Kasus dalam yang diangkat di sini adalah suatu permukaan pada ruang tiga-dimensi
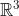
.
Suatu permukaan pada
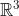
sistem koordinat Cartesis, dapat dinyatakan sebagai
=0})
, yang tentu saja

masing-masing dapat dinyatakan dengan dua parameter, misalnya

sehingga
})
,
})
, dan
})
... .
Agar supaya suatu titik pada permukaan tersebut dapat bergerak menurut lengkungan permukaan tadi, maka yang kita gerakkan adalah dua parameter tadi, yaitu

... , sehingga otomatis nilai

akan otomatis menyesuaikan sedemikian rupa sehingga
=0})
... .
kok Integral 1/dx itu = ln x ...
Sebenarnya tidak seluruhnya merupakan definisi ... . Hampir semua hasil-hasil yang diperoleh dalam matematika itu dapat ditelusuri ... .
Andaikan
=\ln|x|})
, maka
=\lim_{\Delta{x}\rightarrow0}\frac{f(x+\Delta{x})-f(x)}{\Delta{x}}=\lim_{\Delta{x}\rightarrow0}\frac{\ln|x+\Delta{x}|-\ln|x|}{\Delta{x}}}=\lim_{\Delta{x}\rightarrow0}\ln\left|1+\frac{\Delta{x}}{x}\right|^{1/\Delta{x}})
... .
Karena
^{1/\epsilon})
, maka
^{1/\epsilon}\right|^{1/x}=\ln\left|\lim{\epsilon\rightarrow0}(1+\epsilon)^{1/\epsilon}\right|^{1/x}=\ln{e^{1/x}}=\frac{1}{x}})
... .
Karena integrasi merupakan anti-turunan, maka

, dengan

... .
Nomor 2:
Misalkan $z:=e^{ix}$, maka $dz=iz\,dx$ ... .
\[ \cot{x}=i\frac{e^{ix}+e^{-ix}}{e^{ix}-e^{-ix}}=i\frac{z+z^{-1}}{z-z^{-1}}=i\frac{z^2+1}{z^2-1} \] ... .
\[ I=\int_{-\pi}^\pi{\frac{dx}{1+\sqrt{\cot{x}}}}=-i\oint_{S^1}\frac{z^{-1}\,dz}{1+\sqrt{i\frac{z^2+1}{z^2-1}}} \] ... ,
di mana $S^1$ adalah lingkaran berjari-jari 1 dan berpusat di O ... .
\[ I=-i\,2\pi{i}\,\lim_{z\rightarrow0}\,\frac{1}{1+\sqrt{i\frac{z^2+1}{z^2-1}}}=\frac{2\pi}{1+\sqrt{-i}} \] ... .
\[ -i=e^{i(-\frac{\pi}{2}+2n\pi)} \] dengan $n\in\mathbb{Z}$ ... .
\[ \sqrt{-i}=e^{i(-\frac{\pi}{4}+n\pi)}=\cos(-\frac{\pi}{4}+n\pi)+i\sin(-\frac{\pi}{4}+n\pi) \] ... .
\[ I=\frac{2\pi}{[1+\cos(-\frac{\pi}{4}+n\pi)]+i\sin(-\frac{\pi}{4}+n\pi)} \] ... .
\[ I=2\pi\frac{[1+\cos(-\frac{\pi}{4}+n\pi)]-i\sin(-\frac{\pi}{4}+n\pi)}{[1+\cos(-\frac{\pi}{4}+n\pi)]^2+\sin^2(-\frac{\pi}{4}+n\pi)} \] ... .
Berapa nilai dari Int(1/(1+x^4))dx
pada daerah 0 sampai tak hingga?
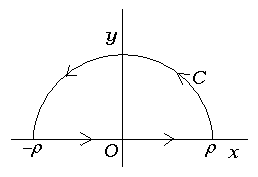
^4}=2\pi\,i\sum_{j=1}^N\,R(z_j)})
... .
\left(z+\frac{1-i}{\sqrt{2}}\right)\left(z+\frac{1+i}{\sqrt{2}}\right)\left(z-\frac{1-i}{\sqrt{2}}\right)})
... .
=R\left(\frac{1+i}{\sqrt{2}}\right)=\lim_{z\rightarrow\frac{1+i}{\sqrt{2}}}\frac{1}{\left(z+\frac{1-i}{\sqrt{2}}\right)\left(z+\frac{1+i}{\sqrt{2}}\right)\left(z-\frac{1-i}{\sqrt{2}}\right)}})
i\sqrt{2}}=\frac{1}{2\sqrt{2}(i-1)}=-\frac{1+i}{4\sqrt{2}}})
... .
=R\left(\frac{i-1}{\sqrt{2}}\right)=\lim_{z\rightarrow\frac{i-1}{\sqrt{2}}}\frac{1}{\left(z-\frac{1+i}{\sqrt{2}}\right)\left(z+\frac{1+i}{\sqrt{2}}\right)\left(z-\frac{1-i}{\sqrt{2}}\right)}})
}=\frac{1}{2\sqrt{2}(1+i)}=\frac{1-i}{4\sqrt{2}}})
... .
=R(z_1)+R(z_2)=-\frac{1+i}{4\sqrt{2}}+\frac{1-i}{4\sqrt{2}}=-\frac{i}{2\sqrt{2}}})
... .
=\frac{\pi}{\sqrt{2}}=2\,\int_{-\infty}^\infty\frac{dx}{1+x^4}})
... .

... .
integral e^(x.lnx) dx 
Permisi ... . Salam kenal ... .

Mula-mula kita per-deret-pangkat-kan dahulu $e^{x\ln{x}}\equiv{x^x}$ ... , yaitu
\[ x^x=\sum_{j=0}^\infty\frac{1}{j!}\,\left(\frac{d^j}{dy^j}(y^y)\right)_{y\rightarrow{h}}(x-h)^j \]
dengan $h$ merupakan suatu bilangan nyata selain nol ... , sehingga $x^x$ berbentuk polinom ... , yang tentu saja dapat di-integral-kan ... .
\[ \int{x^x}dx=\int\sum_{j=0}^\infty\frac{1}{j!}\,\left(\frac{d^j}{dy^j}(y^y)\right)_{y\rightarrow{h}}(x-h)^j\,dx \]
\[ =\sum_{j=0}^\infty\frac{1}{j!}\,\left(\frac{d^j}{dy^j}(y^y)\right)_{y\rightarrow{h}}\int(x-h)^j\,dx \]
\[ =\sum_{j=0}^\infty\frac{1}{(j+1)!}\,\left(\frac{d^j}{dy^j}(y^y)\right)_{y\rightarrow{h}}(x-h)^{j+1}+\textrm{tetapan} \] ... .
Haleluya.